Examples¶
Here you find some examples demonstrating Nanocut’s capablities. You have at least one example for every geometrical body. The molecules had been visualized and rendered using Jmol and Povray.
Clusters (0D)¶
Octahedral diamond cluster¶
A nice octahedral shaped diamond cluster for your quantum bit project:
[geometry]
lattice_vectors:
0.00000000 1.78500000 1.78500000
1.78500000 0.00000000 1.78500000
1.78500000 1.78500000 0.00000000
basis:
C 0.00 0.00 0.00
C 0.25 0.25 0.25
basis_coordsys: lattice
[polyhedron: 1]
planes_normal:
1 1 1 5
-1 1 1 5
1 -1 1 5
-1 -1 1 5
1 1 -1 5
-1 1 -1 5
1 -1 -1 5
-1 -1 -1 5
planes_normal_coordsys: cartesian
You should obtain a 165 atom cluster as in Figure Octahedral diamond cluster.
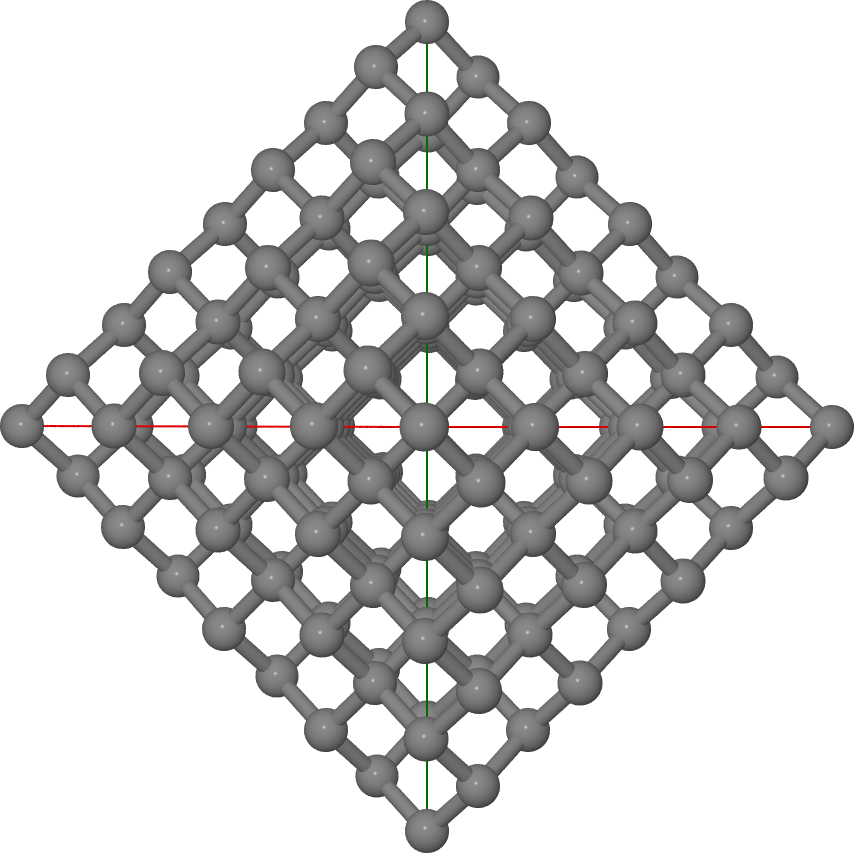
Octahedral diamond cluster
Spherical diamond cluster¶
The same as above but creating a spherical diamond nanoparticle with the a radius of 2 nm:
[geometry]
lattice_vectors:
0.00000000 1.78500000 1.78500000
1.78500000 0.00000000 1.78500000
1.78500000 1.78500000 0.00000000
basis:
C 0.00 0.00 0.00
C 0.25 0.25 0.25
basis_coordsys: lattice
[sphere: 1]
radius: 20
The resulting cluster is rather big, but looks indeed spherical (see Figure Spherical diamond cluster).
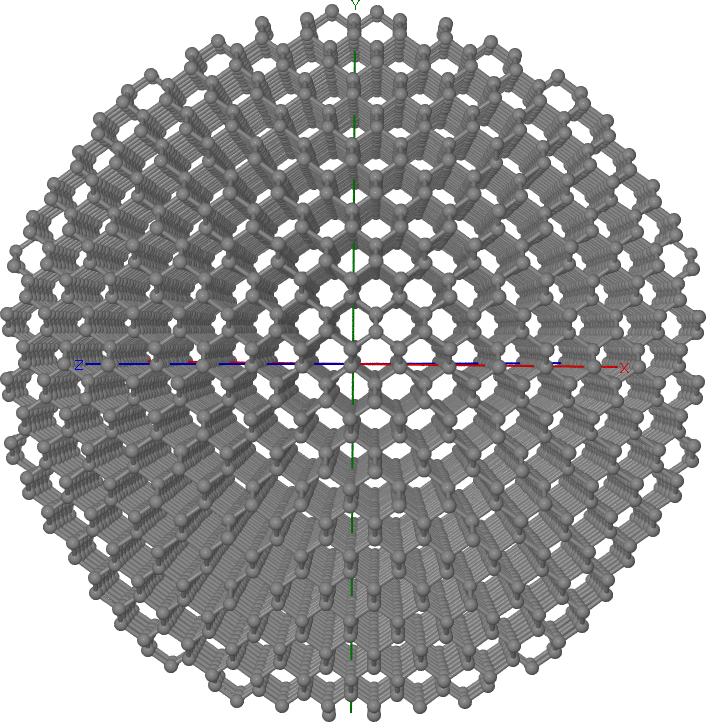
Spherical diamond cluster
The cluster you obtain this way is atom centered. If you wanted a Td-site centered sphere instead (its center being in the origin), you should shift the basis atom coordinates by the appropriate amount using the shift_vector option in the [geometry] section:
[geometry]
lattice_vectors:
0.00000000 1.78500000 1.78500000
1.78500000 0.00000000 1.78500000
1.78500000 1.78500000 0.00000000
basis:
C 0.00 0.00 0.00
C 0.25 0.25 0.25
basis_coordsys: lattice
shift_vector: 0.25 0.25 0.25
shift_vector_coordsys: lattice
[sphere: 1]
radius: 10
This results in a spherical, Td-centered cluster as shown in Figure Spherical Td-centered diamond cluster (the cluster radius had been decreased to 10 Angstrom).
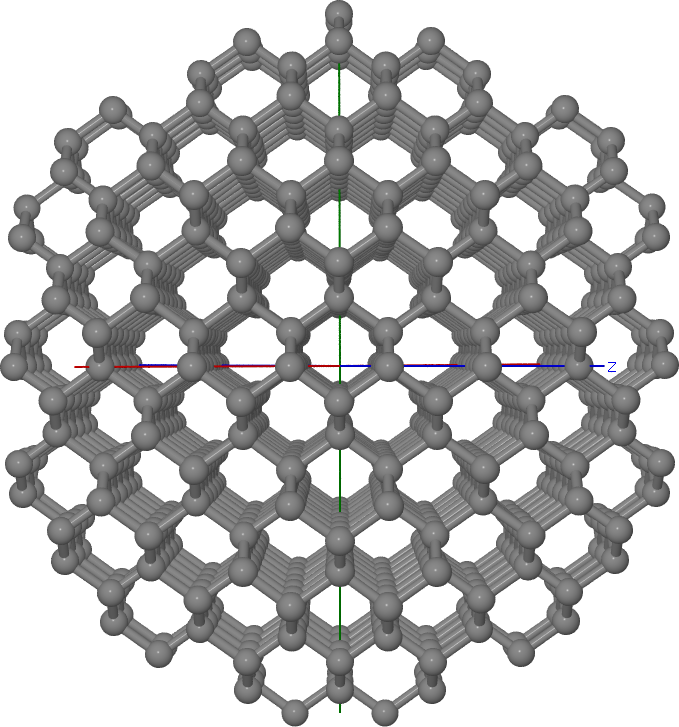
Spherical Td-centered diamond cluster
Cylindrical silicon carbide cluster¶
It is questionable, whether a conical 3C-SiC along the [111] direction is a meaningful atomistic object, but Nanocut can definitely produce such one, if requested:
[geometry]
lattice_vectors:
0.00000000 2.18000000 2.1800000
2.18000000 0.00000000 2.18000000
2.18000000 2.18000000 0.00000000
basis:
Si 0.00 0.00 0.00
C 0.25 0.25 0.25
basis_coordsys: lattice
[cylinder: 1]
point1 = 0 0 0
point2 = 10 10 10
point2_coordsys = cartesian
radius1 = 5
radius2 = 9
This would then look something like Figure 3C-SiC truncated cone.
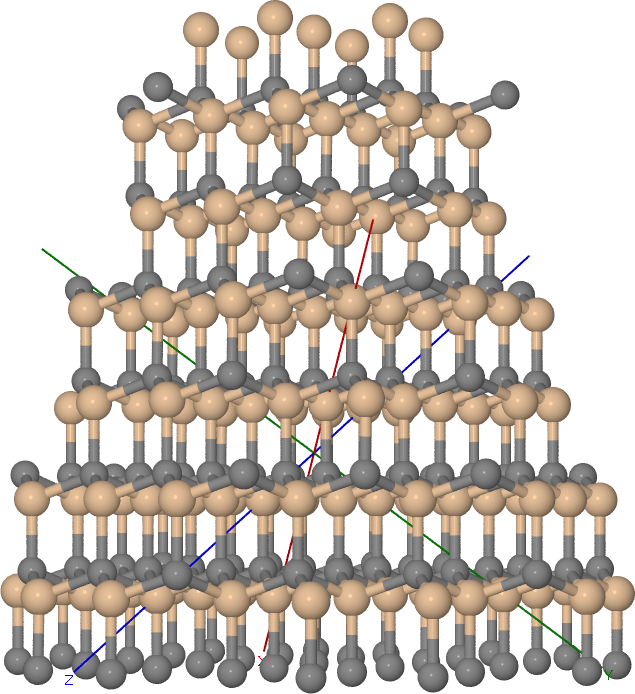
3C-SiC truncated cone
Nanowires (1D)¶
Cylindrical sodium chloride [111] wire¶
An input for a salty wire might look as
[geometry]
lattice_vectors:
0 2.83 2.83
2.83 0 2.83
2.83 2.83 0
basis:
Na 0 0 0
Cl 0.5 -0.5 0.5
[periodicity]
period_type: 1D
axis: 4 4 4
[periodic_1D_cylinder:1]
radius: 10
and should result in the structure in Figure NaCl wire.

NaCl wire
Every geometrical object allows the flag additive, which you can set to false in order to substract something from the previous structure. In the case of the NaCl wire, one can use that to create a wire being empty in the middle:
[geometry]
lattice_vectors:
0 2.83 2.83
2.83 0 2.83
2.83 2.83 0
basis:
Na 0 0 0
Cl 0.5 -0.5 0.5
[periodicity]
period_type: 1D
axis: 4 4 4
[periodic_1D_cylinder:1]
radius: 10
# Second cylinder is subtracted from the previous one
[periodic_1D_cylinder:2]
additive: false
radius: 5
With this input you should obtain a nanowire with an empty core shell as in Figure NaCl wire with an empty core.
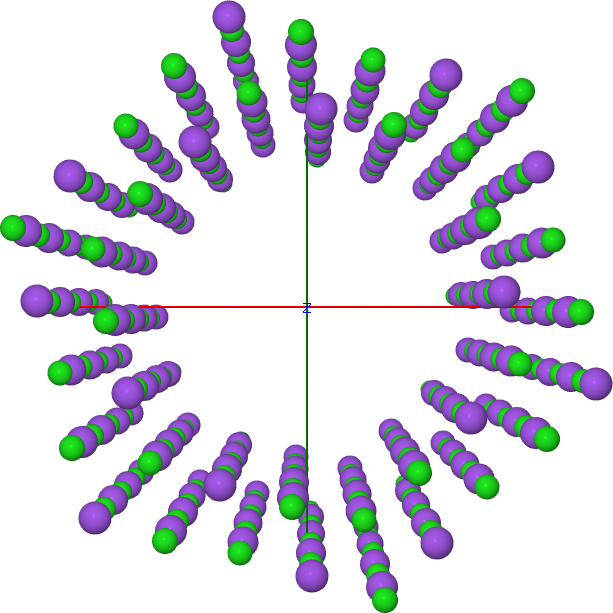
NaCl wire with an empty core
Rectangular rutile [001] wire¶
The input below should create the primitve cell of a rutile [001] nanowire:
[geometry]
lattice_vectors:
4.67700000 0.00000000 0.00000000
0.00000000 4.67700000 0.00000000
0.00000000 0.00000000 2.99900000
basis:
Ti -0.5 0. 0.
Ti 0. 0.5 0.5
O -0.1986603 0.3013397 0.
O 0.1986603 0.6986603 0.
O 0.3013397 0.1986603 0.5
O -0.3013397 0.8013397 0.5
basis_coordsys: lattice
[periodicity]
period_type: 1D
axis: 0 0 1
[periodic_1D_prism: 1]
planes_normal:
1 1 0 16.5
1 -1 0 16.5
-1 1 0 16.5
-1 -1 0 16.5
planes_normal_coordsys: cartesian
The resuling structure should look something like Figure Rutile nanowire.
![Rutile [001] nanowire](_images/r001_d2d_sq.png)
Rutile nanowire
Slabs (2D)¶
Diamond (100) surface¶
Creating a diamond slab with a thickness of 12 atoms and a 4x4 surface supercell cell would require an input like this:
[geometry]
lattice_vectors:
0.00000000 1.78500000 1.78500000
1.78500000 0.00000000 1.78500000
1.78500000 1.78500000 0.00000000
basis:
C 0.00 0.00 0.00
C 0.25 0.25 0.25
basis_coordsys: lattice
[periodicity]
period_type: 2D
axis:
0 0 1
1 -1 0
axis_repetition: 4 4
[periodic_2D_plane:slab]
thickness: 12
Please note, that Nanocut always gives the smallest possible unit cell, so that the axis_repetition opion had to be used to enlarge it. As result, you would obtain the slab in Figure Diamond slab.
![Diamond [100] slab](_images/diamond100.png)
Diamond slab
Diamond (211) surface¶
An alternative way of determining the surface plane of a slab is to specify its Miller indices. Since the Miller indices are usually given with respect to the conventional Bravais lattice, you should consider the usage of the bravais_cell option in the [geometry] section for non-conventional lattices. (The appropriate transformation matrix can be determined via Nanocut, see the section Automatic Bravais cell search). For the 211 diamond surface the input would look as the following:
[geometry]
lattice_vectors:
0.000 1.785 1.785
1.785 0.000 1.785
1.785 1.785 0.000
basis:
C 0.00 0.00 0.00
C 0.25 0.25 0.25
bravais_cell:
-1 1 1
1 -1 1
1 1 -1
[periodicity]
period_type: 2D
miller_indices: 2 1 1
[periodic_2D_plane:slab]
thickness: 10
The resuling structure should look something like Figure Diamond 211 surface.
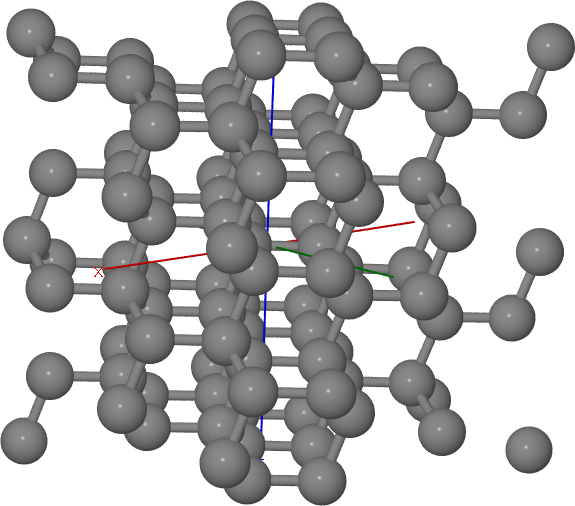
Diamond 211 surface
Supercells (3D)¶
3C-SiC, 64 atom cubic supercell¶
In order to build a 64 atom cubic supercell of 3C-SiC, the lattice vectors of the base lattice must be combined to yield a cubic superstructure of the right size:
[geometry]
lattice_vectors:
0.00000000 2.18000000 2.1800000
2.18000000 0.00000000 2.18000000
2.18000000 2.18000000 0.00000000
basis:
Si 0.00 0.00 0.00
C 0.25 0.25 0.25
[periodicity]
period_type: 3D
axis:
-1 1 1
1 -1 1
1 1 -1
axis_repetition: 2 2 2
[periodic_3D_supercell:1]
shift_vector: -0.5 -0.5 -0.5
In the input above, the resulting supercell had been shifted by the half of the diagonal of the orginal unit cell, to make the supercell look more compact (see Figure Cubic 3C-SiC supercell).
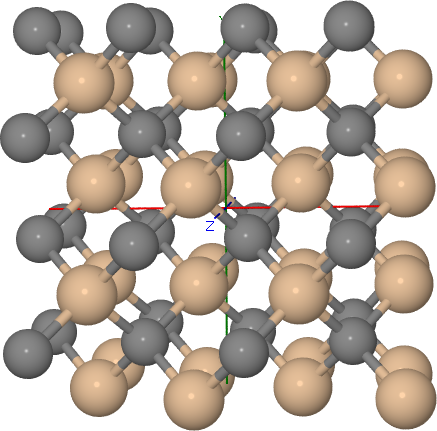
Cubic 3C-SiC supercell
Automatic Bravais cell search¶
Nanocut can help you to find the transformation matrix, which creates the Bravais lattice from the primitive lattice. For example, in order to get the cubic conventional cell of SiC, you should enter the following configuration file:
[geometry]
lattice_vectors:
0.00000000 2.18000000 2.1800000
2.18000000 0.00000000 2.18000000
2.18000000 2.18000000 0.00000000
basis:
Si 0.00 0.00 0.00
C 0.25 0.25 0.25
[periodicity]
period_type: 3D
superlattice:
1.0 0.0 0.0
0.0 1.0 0.0
0.0 0.0 1.0
[periodic_3D_supercell:bravais]
In the output of Nanocut you should see the transformation matrix:
Axis with respect to primitive lattice:
-1 1 1
1 -1 1
1 1 -1
Additionally the resulting geometry file would contain the simple cubic 8 atom unit cell.